
Physics - Vertical Motion - Basic Falling Object Problems-- How are we doing now?
OPENING QUESTION: Today we'll do a couple of timed exercises to see how we're doing with these pesky falling object problems.
#1) VERY basic: You're lying on your back in a pretty meadow on a nice calm spring day with your trusty wrist-rocket sling shot and a supply of frozen grapes.
You launch a grape upwards with an initial velocity of 39.50 m/s.
a) How high does it go
b) How long does it take to get there.
I'll set the timer for 5 minutes - Go.
We'll peer grade these
#2) Intermediate: You drop a frozen grape from the top of a 550 m structure.
a) How long does it take before it goes *splat* ?
b) How fast is it going the tiniest fraction of a second before it hits the ground?
I'll set the timer for 10 minutes - Go.
ARNING OBJECTIVES:
- I will evaluate my ability to solve falling object problems during today's class
CALENDAR:
Vertical motion test on Thursday (NOT to include projectile motion)
WORDS O' THE DAY:
- gravity! gravity! gravity!
FORMULAE OBJECTUS:
-
a = (vf - vi)/(tf - ti) (definition of acceleration)
- g = 9.81 m/s2 (acceleration an object experience on Earth) ONLY present in vertical motion (Y axis) problems
1) vfy = viy +agt
2) yf = yi + viyt + 1/2agt2
3) vfy2 - viy2 = 2ag∆y
Let's go back to this MOST informative (AND COMPLEX) graphic of a falling object problem:
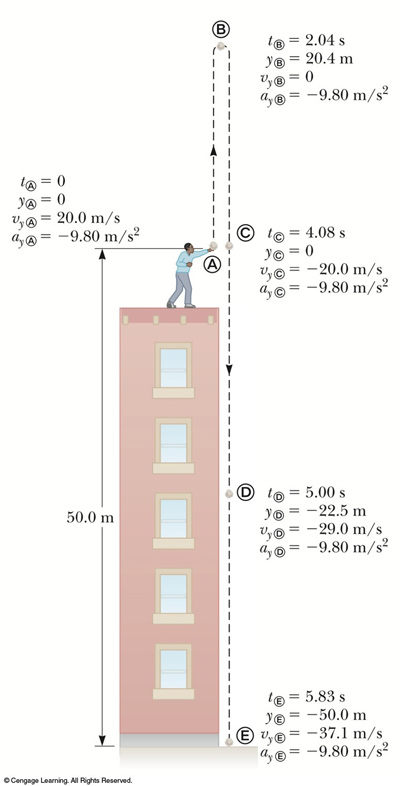 |
There are a couple of things to keep in mind when we evaluate motion in 1 dim (vertically):
Here's a pretty complex graphic. Look at JUST parts A and B. What can you determine from the values shown there? |
Let's take a look at a couple of practice problems in our book: #40, 42 and 43.